Covid19mathblog.com
A worthwhile podcast Joe Rogan and Dr. Sanjay Gupta – not all covid – but a good discussion on risk/reward – including a discussion on Cannabis. https://open.spotify.com/episode/6rAgS1KiUvLRNP4HfUePpA?si=izgzzVthSPao8dCxwzCUCA
The one note Dr. Gupta brought up multiple times and justified the social need to get the covid vaccination – “Unvaccinated 8 Times more likely to get INFECTION”. So I spent awhile searching for this study as it does makes sense for a social requirement for getting vaccinated if true.
The study is done by the CDC Vaccine Effectiveness Team – here it is: https://www.cdc.gov/mmwr/volumes/70/wr/mm7037e1.htm?s_cid=mm7037e1_w#T1_down
First to note and hopefully someone tells Dr. Gupta – the report conclusion is 5X not 8X – perhaps the original document is 8X but this is the study – https://twitter.com/annezinkmd/status/1424229063460212738
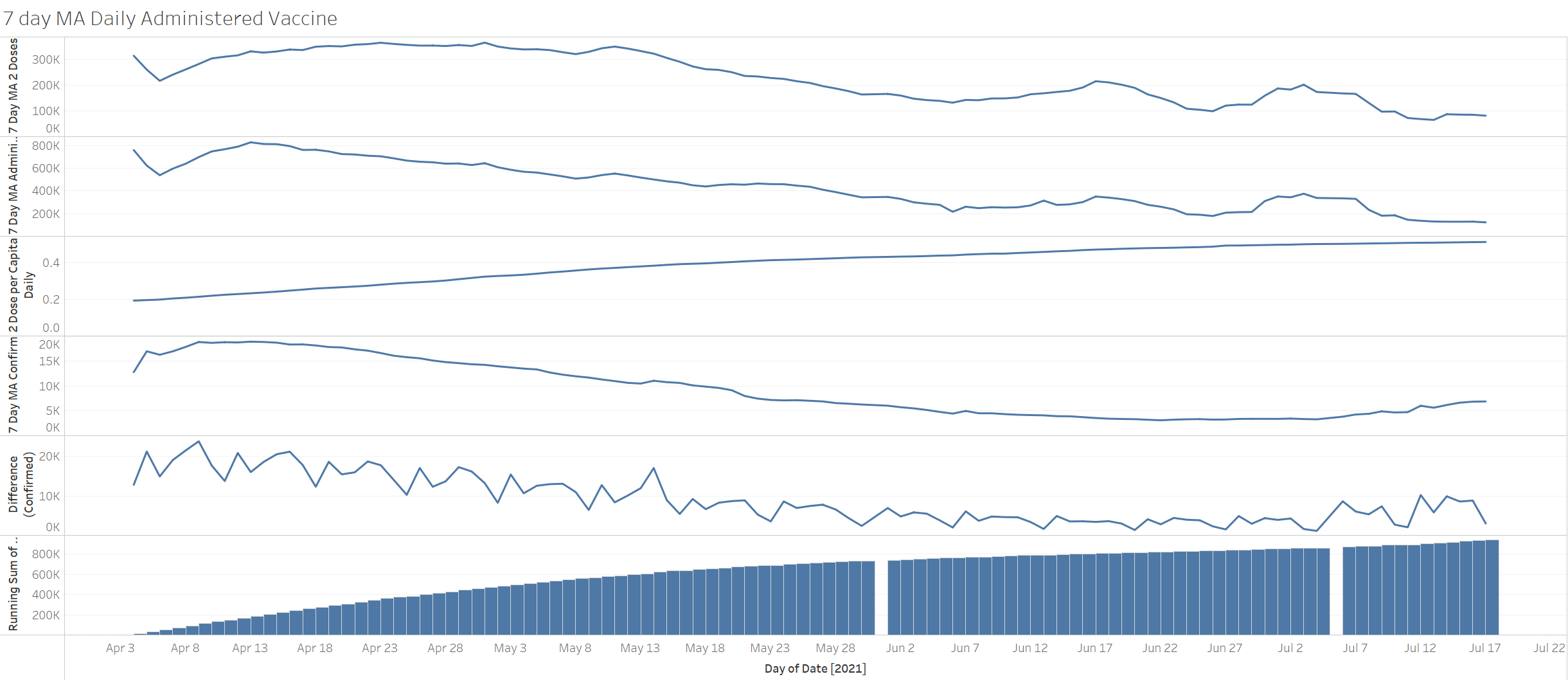
There is no link to the data – and I have found no place to show the breakout of the confirmation between vaccinated or not vaccinated. However by the 13 states I could go through the data I had and extrapolate from the per capita vaccination I had for each state. The data April 4th- June 19th is quite irrelevant given the level of vaccination was extremely low in April with corresponding increasing vaccination rate.
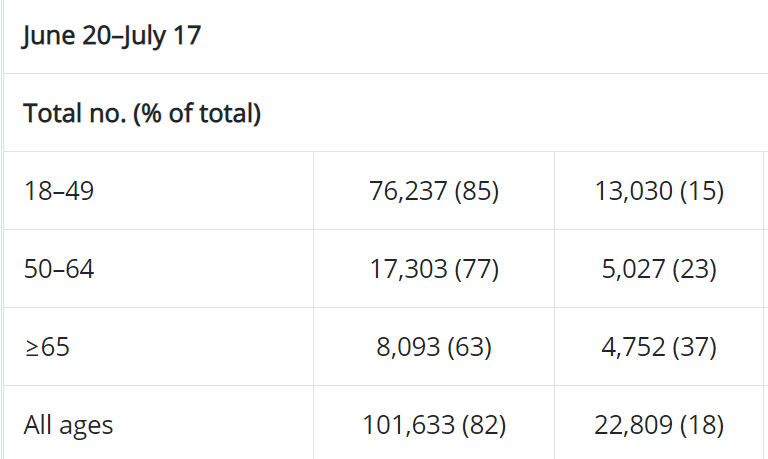
So the data from June 20-July 17th in their table shows the following with the first column represent incidences reported that are unvaccinated and the next vaccinated. The total 101633/22809 = 4.45X – so they round up to 5X
Since I don’t have their vaccinated and unvaccinated data and are suspect they do have it too in the detail needed – I computed the daily vaccinated/unvaccinated using the vaccinated per capita which I have daily. I also use a 14 day lag on the vaccinated rate given one doesn’t qualify vaccinated without a 14 day spread.
My total confirmed case in my data series is 123,161 – not to bad vs. 124,442 from the above table from the report. Based on state by state and 14 day lag the total incidence of vaccinated and unvaccinated ASSUMING natural even distribution with the separation purely based on a level of unvaccinated started low and confirmation slowing down in the later part the total vaccinated incidence comes out 45K vs. unvaccinated 78K – so this is 1.7X – so naturally there was already supposed to be a spread of incidence of more unvaccinated just by shear population that had not gotten vaccinated. So perhaps in effect IF the logic held true the normalized impact of the unvaccinated vs. vaccinated is not 5X but 4.45-1.73= 2.7 – so perhaps the statement can be made if you are unvaccinated you are 2.7X more likely to get a CONFIRMATION of covid. I changed the word from INFECTION TO CONFIRMATION as this is a slight of hand trick they have played. You NEED to take a test to be confirmed and shown as an infection as the number of confirmed case is equivalent to their definition of infection. HOWEVER think about it IF you have taken the vaccine and are infected and are asymptomatic what are the ODDS you would go take a test to be confirmed!
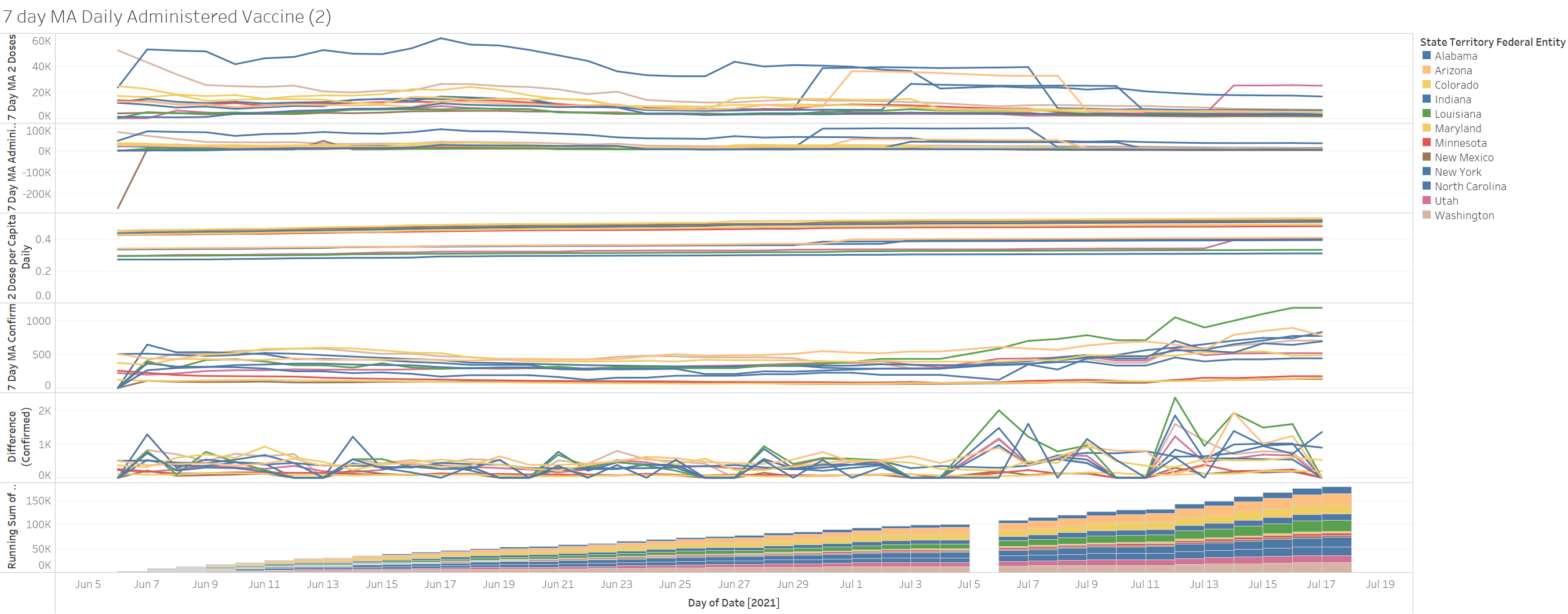
In addition IF their statement was true then how come the more vaccinated counties don’t clearly show a delineation from the less vaccinated – I mean its as high as 8X-2.7X more likely to be confirmed IF you are unvaccinated per their report.
CONCLUSION – ITS NOT TRUE – FAKE STAT of reference. IF the vaccinated are more asymptomatic (TRUE STATEMENT – NOTED BY SEVERAL STUDIES) then when they are infected the odds of them going to take a test to confirm covid is likely approaching 0. They cannot make a claim that unvaccinated is ANY multiple more likely to be infected base on this analysis. They can make a claim the unvaccinated are likely to get tested and be confirmed at 2-5X more than a vaccinated person – but this means nothing in terms of infection and transmission. If you don’t see that you are likely in confirmation bias land to try to prove the point vaccination reduces transmission and hence everyone should get vaccinated. The data is clear it does not and the logic to conclude that is wrong per the above analysis. Perhaps another study may prove this to be the case – but certainly not the above report method.